 Мой друг-математик писал как-то раз статью и прервался на слове "матожидание". Его дочка, недавно освоившая чтение,
заглянула на монитор и прочла это слово. Попыталась его понять как могла, результатом стал вопрос:
"Папа, а от кого ты мат ожидаешь?"
Мой друг-математик писал как-то раз статью и прервался на слове "матожидание". Его дочка, недавно освоившая чтение,
заглянула на монитор и прочла это слово. Попыталась его понять как могла, результатом стал вопрос:
"Папа, а от кого ты мат ожидаешь?"
Небольшое продолжение предыдущей статьи на
тему матожидания и как иногда бывает.
Вначале я все же повторю азбучную истину из теорвера, которую иногда все же забывают.
Среднее арифметическое некоторой выборки - это ни в коем случае не матожидание. Это - выборочное среднее.
Для некоторых
распределений, например для нормального, можно доказать что выборочное среднее значение - лучшая оценка матожидания,
но это ОЦЕНКА, а не само матожидание.
Распределение вероятностей и, соответственно, матожидание результат
физических свойств системы, например,
матожидание игры в реальную, неидеальную, монетку или рулетку, определяются их физическими свойствами. Теоретически, очень
теоретически, можно ни разу не бросая монетку, а только тщательно изучив ее, сказать каким будет матожидание в
схеме Бернулли. Конкретный результат игры и конкретное выборочное среднее - это реализация свойств физической системы.
Так же нельзя путать вероятность (определяется физикой), статистическую частоту (объективная величина - сколько раз
явление произошло) и оценку вероятности (существенно субъективная вещь, которая может быть самой разной, от основанной
на статистике и правильной математике, до "видный эксперт Х. заявил, что вероятность кризиса в этом году с падением
индекса вдвое равна 87%).
Да, если система сложная, посложнее монетки-рулетки, особенно если в ней участвует хотя бы один человек, и уж тем
более, как в случае экономических задач, не один, а огромное количество - вероятности конечно же есть, матожидание
наверное есть (но может и не быть), вот только вы их не узнаете никогда. Хуже того, сколь-нибудь точная оценка в
большинстве случаев невозможна. Собственно, поэтому меня всегда напрягает
термин "матожидание" в контексте торговых систем и экономики. Оно-то может и быть, но вы его не узнаете! Более того,
точно не оцените. И оно может сильно измениться, пока вы его оцениваете и планируете на нем обогатиться.
Я уже писал о том, насколько усложняется жизнь в типичных для трейдинга ситуациях, когда матожидание (μ) мало
по сравнению с σ , в обычной жизни типичны обратные ситуации, когда σ много меньше μ. Как пользоваться,
к примеру, вольтметром, который измеряет сотни вольт с погрешностью в десятые понятно, а вот если наоборот?..
Однако это не единственная проблема. И их даже не две, с учетом извечной проблемы нестационарности.
Речь пойдет о… Ну давайте сохраним интригу ;).
 Взгляните на эту гистограмму, это реальная гистограмма большого набора данных (100 тысяч)
Форма кривой колоколообразная, и в чем-то похоже на классическое нормальное распределение, но это очень "ненормальное"
распределение.
Взгляните на эту гистограмму, это реальная гистограмма большого набора данных (100 тысяч)
Форма кривой колоколообразная, и в чем-то похоже на классическое нормальное распределение, но это очень "ненормальное"
распределение.
Если ориентироваться на глаз, то видно, что распределение симметричное (вроде как), одномодальное, с ярко выраженной
модой (местоположение пика), медианой ну и, видимо, матожидание там же.
Опыт работы с нормальными или "квазинормальными" распределениями подсказывает, что можно взять, да и посчитать среднее
арифметическое, выборка не просто большая, а очень большая, для трейдинга просто огромная, если предположить, что
это результаты ежедневной торговли, то они покрывают период в почти 400 лет. Поэтому все должно хорошо и красиво сойтись.
Ну что, пробуем? Результатом, судя по гистограмме, должно быть матожидание немного положительное, близкое к нулю.
Но у нас получилось -1.446, что как-то совсем не похоже на правду. Странно.
А давайте сделаем такой эксперимент, будем идти начиная с самого первого значения по одному шагу до последнего и на
каждом шаге считать среднее арифметическое известной части. В случае с нормальным распределением это среднее значение
будет вначале метаться, но довольно быстро стабилизируется около матожидания.
Таблица на 100 тысяч строк это слишком, поэтому я представляю выборочные результаты, достаточные для того, чтобы
понять, что происходит. Сначала каждый десятый, потом каждый сотый, тысячный, десятитысячный.
| N | Среднее арифм. |
| 10 | 0.506677507 |
| 20 | 10.15510935 |
| 30 | 6.058863908 |
| 40 | 4.226630457 |
| 50 | 3.309173297 |
| 60 | 2.757305625 |
| 70 | 2.446337581 |
| 80 | 2.07481715 |
| 90 | -2.217449425 |
| 100 | -2.355820795 |
| 200 | -0.976619355 |
| 300 | -0.603667725 |
| 400 | -0.510637011 |
| 500 | -1.00814289 |
| 1000 | -0.595856024 |
| 2000 | 0.549189574 |
| 3000 | 1.125594193 |
| 4000 | 1.01037185 |
| 5000 | 0.839456199 |
| 10000 | 1.425875696 |
| 20000 | -3.536047624 |
| 30000 | -2.116909618 |
| 40000 | -1.428322431 |
| 50000 | -1.175317401 |
| 60000 | -1.287852029 |
| 70000 | -1.210421058 |
| 80000 | -0.917291055 |
| 90000 | -1.057539779 |
| 100000 | -1.446037771 |
Результаты обескураживающие. Среднее и не думает стабилизироваться, оно мечется "как бешеная стрелка
осциллографа" (цитируя одну небезызвестную мадам). Факир был пьян и фокус не удался. Может 100 тысяч мало? Увы,
теория говорит, что на любой, сколь угодно большой выборке этого прекрасного распределения стабилизации среднего
не будет, оно будет метаться, периодически уходя иногда далеко, и даже очень далеко..
Самое забавное, что если вместо среднего арифметического будем считать медиану шага за шагом уточняя ее, то все получится
сильно лучше. Схождение будет медленное, но все же будет, фокус удался.
| N | Медиана |
| 10 | -1.891992444 |
| 20 | -0.942270042 |
| 30 | -0.387852949 |
| 40 | -0.387852949 |
| 50 | -0.261349111 |
| 60 | -0.240057587 |
| 70 | -0.136160179 |
| 80 | -0.157651983 |
| 90 | -0.292900845 |
| 100 | -0.292900845 |
| 200 | -0.273610735 |
| 300 | -0.087501967 |
| 400 | -0.142425988 |
| 500 | -0.073011031 |
| 1000 | 0.04258281 |
| 2000 | 0.03576348 |
| 3000 | 0.069873012 |
| 4000 | 0.125653989 |
| 5000 | 0.112460561 |
| 10000 | 0.093318582 |
| 20000 | 0.108099061 |
| 30000 | 0.121505686 |
| 40000 | 0.121995053 |
| 50000 | 0.125685901 |
| 60000 | 0.126190918 |
| 70000 | 0.13065827 |
| 80000 | 0.130050034 |
| 90000 | 0.129241421 |
| 100000 | 0.132911591 |
Для самых любопытных, здесь лежит полная выборка
из 100,000 значений, использованная для экспериментов.
В чем же дело? Представленная выборка была сгенерирована из одного прекрасного распределения Коши.
Это распределение абсолютно несложное, это не какой-то заумный математический выверт.
Например, если плотность вероятности пропорциональна 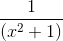 , то это частный случай распределения Коши.
Главная достопримечательность его в том, что матожидание и дисперсия отсутствуют. Они не определены, иногда
говорят что бесконечны. При том, что "на глазок" матожидание вполне себе существует.
, то это частный случай распределения Коши.
Главная достопримечательность его в том, что матожидание и дисперсия отсутствуют. Они не определены, иногда
говорят что бесконечны. При том, что "на глазок" матожидание вполне себе существует.
Именно из-за бесконечности матожидания у нас получается такой странный эффект со средним арифметическим.
Эффект, что среднее мечется и не находит медиану (совпадающую с модой), в некотором смысле сродни знаменитому
Санкт-Петербургскому парадоксу Бернулли.
Пример реальной ситуации, где возникает распределение Коши. Допустим, есть радиоактивный источник, равномерно излучающий
во все стороны. Вы с дозиметром двигаетесь по прямой, не проходящей через источник. Интенсивность излучения нарастает и
достигает максимума, когда расстояние до источника минимально, потом начинает убывать. Показания дозиметра в зависимости
от местоположения на этой прямой, будут распределены по Коши.
Из всего этого следует два очень важных вывода: во-первых, снова повторюсь, медиану использовать обычно лучше и надежнее,
чем среднее арифметическое (хотя, конечно, использовать с умом и понимая задачу и понимая, что медиана - не панацея).
А вот второе следствие имеет куда
как более печальное влияние на всю финансовую математику, по масштабности производимого эффекта может тягаться с проблемой
нестационарности, о нем в следующем посте, уже на днях ;).
P.S. Немножко математики
Немного математических забавностей про распределение Коши.
Плотность распределения в общем виде задается формулой:
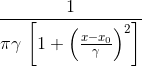
Матожидание можно посчитать по формуле:
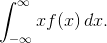
но этот интеграл Лебега не существует, или, если угодно бесконечен.
Чтобы придать пикантности ситуации следующий предел существует и дает вполне ожидаемый результат:
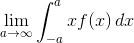
А этот предел 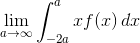 тоже существует и дает совершенно неожиданный
результат, несовпадающий с предыдущим пределом.
тоже существует и дает совершенно неожиданный
результат, несовпадающий с предыдущим пределом.
Распределение Коши нередко возникает в разных областях физики, там оно фигурирует под именем распределения Лоренца
(в классической физике) или Брейта-Вигнера в одноименной формуле. Но есть и совсем простой пример: если две
независимых случайных величины X и Y распределены нормально с μ=0, σ=1, то их отношение X / Y будет
внезапно распределено по Коши.